Unraveling the Floating-Point Puzzle: Ensuring Seamless Model Deployment
If you've ever tried to deploy a model to a production environment, this may sound familiar: You've trained your model, and it does well on your research dataset. Things are looking really good. Then the engineers integrate it into the product, and discrepancies start appearing on the same data. This is terrible timing because by now, it's time to deliver a product, and you're scrambling to figure out what's going wrong.
If this resonates with you, then know you are not alone. This is a pretty common problem that typically stems from issues related to floating-point precision.
In this blog, I will look to better understand the problem, explore possible remediations and make recommendations on how to avoid this going forward.
Are Floating-Point Calculations Deterministic?
When data discrepancies appear, the first thing that comes to mind — or that a teammate might say — is along these lines: "Maybe there's something weird going on with the floating-point arithmetic." This is often true, so it’s a logical starting point as you investigate what’s going wrong. However, there remains a lot of mystery surrounding floats, which can raise the question of whether floating-point precision is deterministic.
In short, yes, the precision of floating-point arithmetic is deterministic as there is no degree of randomness added in when calculating operations on floating-point values. The exact same operation run multiple times will in fact achieve the same result — and the computer satisfies Einstein’s definition of not being insane.
What Can Go Wrong with Floating-Point Arithmetic?
So, if the precision of floating-point arithmetic is deterministic, what can possibly go wrong? There are several ways in which these calculations can go awry when certain components are unwittingly not held constant.
And although there are plenty of good resources out there to describe the following in further detail, here are a few examples that you could consider investigating:
- Check the Execution Order: A x B x C is not necessarily equal to A x C x B. This can be a problem if operations are run in parallel, where the order of execution is variable, and can result in differences between running such computations.
- Consider the Platform: Different operating systems, programming languages, compilers of those programming languages, and hardware that the computations are performed on can all add a slight degree of variation to how floating-point arithmetic is implemented. Changing any of these components can change the results.
- Investigate Possible Truncation: Some programming languages such as C++ may automatically truncate a highly precise initial value into one with less precision, unless higher precision is specified. This will, for obvious reasons, change the expected results of floating-point operations between platforms.
- Watch for Quantization: Similar to truncation, sometimes in the process of converting models to more performant formats, aspects of quantization will be applied to various layers and computations. This strategically decreases runtimes but can also cause small changes to the results.
What's the Impact?
Ideally when we deploy a model, it will just work the way we expect, and customers will be happy. If this isn’t the case, we want to easily remediate issues, so problems don't escalate. The last thing we want is for the model to perform unpredictably. If the model outputs one class in the research phase for example, but a different class in production, we have a problem on our hands.
If the floating-point arithmetic is being handled slightly differently between platforms, this can be a real consideration and can lead to unexpected and hard to mitigate behaviors.
How do we fix Floating-Point Discrepancies?
Now that I’ve explored possible causes of data discrepancies, let’s examine a few ways you can remediate the issue:
Execution Order: Find alternative ways to ensure that a parallelized process will collect components, but predictably order the computations to refrain from inconsistent outcomes.
Platform: Minimize the difference between the platforms ensuring shared libraries remain in sync, run on similar hardware, etc.
Truncation: Ensure that whatever calculations are being applied in research and in production, that consistency of the results is achieved every step of the way.
Quantization: If the model is to be converted into an alternative format(s) for production purposes, ensure example outputs are stored for each conversion.
Reduce Complexity: Remove any operations that serve no practical purpose. For example, this could mean normalizing data that's already normalized, or perhaps normalizing data that need not be, based on the models that will operate on them. This will remove opportunities for added accumulated errors.
Hopefully it is mission accomplished at this point but that all sounds rather tedious. It would be great if there was an easier way — and there is.
Do you really Need That Much Precision?
At the heart of it, the main source of the problem is that the model learned to split on the features at a very granular level, such that when floating-point arithmetic is inconsistent, the predictions end up being off. What happens if we don't let the model ever dig that deep in the first place?
Consider the platform you are trying to run on. Oftentimes, there will be a known amount of precision used to consider as tolerably different. If unknown, the fifth or sixth decimal place is often used in standard libraries as this tolerance baseline. Instead of training a model, and trying to find the ways the platforms start to deviate on the precision every step of the way, how about we just limit the precision of the features to the precision that the platform will willingly consider, within tolerance? I’ve personally tried this approach, and it works fairly well.
Here’s an example of how we could validate whether this additional precision was providing any value if the platform is usually expected to match results up to the 6th decimal place:
Train Model A on all the precision available.
Train Model B on the same input data that has been rounded to 6 decimal places.
Choose your favorite metric to see how well these models compare (likely involving ROC Curves, FPR, FNR, or other metrics)
If Model B is close enough to Model A , then ship model B.
Model B will have demonstrated its ability to deliver the same desired outcomes to customers as Model A without the same unpredictability in its efficacy based on the platform the model is deployed on. Otherwise, see if there is a way to tease out the difference from different feature engineering steps, or the other remediations I listed earlier. Most of the time, this will not be necessary!
The delta between Model B and Model A:
- This may be the same if the model never needed that level of precision.
- It may be slightly worse if that additional precision was necessary to tease out some more difficult points to classify.
- It could be slightly better if the precision reduction acted as a form of regularization.
Additional Floating-Point Data Considerations
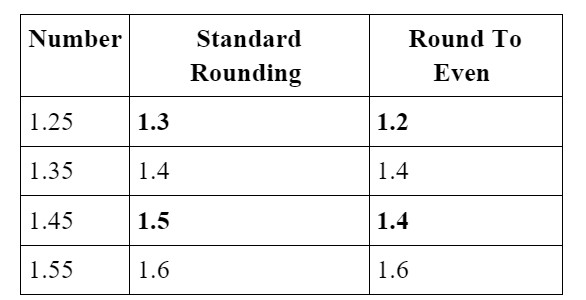
Rounding
Rounding is not as straightforward as one would expect. There are some libraries that will use a "Round to Even" methodology that differs from how we typically round numbers. Let's consider rounding the following numbers to one decimal place using a standard rounding scheme, vs. "Round to Even."
If we use rounding, we will need to make sure it’s the same in production, otherwise we will have inadvertently added another floating-point error to our process!
Cost
If training multiple models is too expensive, explore whether it matters if the predictions are sometimes inconsistent.
- If so, train one model with reduced precision and handle any model errors with the remediation strategy that was going to be used anyways for the inevitable gaps a model will have.
- If not, train with available precision. It could be that a generative model may occasionally switch a predictive token or shade of a pixel, but perhaps not detrimentally so.
Quantization
Quantization Aware Training is similar to rounding but can operate on more elaborate quantization schemes such as moving from float to integer inputs. We may quantize a model so that it can run faster on production, but it may also introduce floating-point arithmetic errors in doing so.
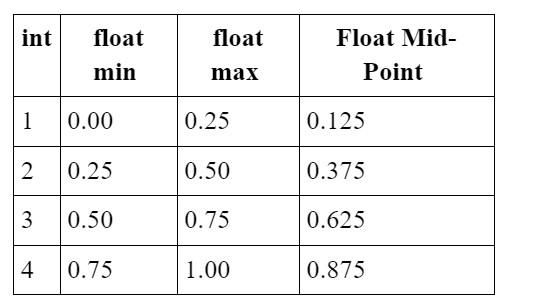
As an example, let's consider a simplistic case where we want to represent float values between 0 and 1, but they will later be quantized as integers between 1 to 4 inclusive. The mapping between those floating point to integer values would look as follows:
Instead of using the original full range of floats from 0 to 1 as features, we would replace the features with the "float mid-point" and train with those. Then when the model is later quantized, there should be very limited precision loss as the model was "aware" that it would be quantized, and makes its training data adhere to the expected quantization. This can result in a model that is less prone to floating-point errors, and one that has improved the efficiency of inference, if needed for the desired application.
Conclusion
As you can see, there are several ways floating-point arithmetic, truncation, rounding and other errors can be introduced during various stages between feature engineering to model inference. Instead of fighting to ensure each of the possible sources of error are mitigated, one can simply reduce the precision of the inputs to the level that can be realistically maintained on a production system. This allows you to train a model, deploy it, and sleep soundly at night — by eliminating the unexpected model predictions that can be linked to the floating-point puzzle.
About Steven Henkel
Steven Henkel is a Principal Data Scientist at BlackBerry.